Par Laurent J., technico-commercial chez Materiel.net depuis 10 ans, né entre deux enceintes et audiophile jusqu’au bout des orteils au grand dam de sa femme et de son banquier. Également grand collectionneur de musique de tout horizon (mais surtout de Soul, Jazz et Funk ) et joueur invétéré ( et vétéran ) de jeux vidéo.
- Audio : de l’intérêt du Hi-Res (page 1)
- Audio : de l’intérêt du Hi-Res (page 2)
Si il y a bien une chose qui a fait couler beaucoup d’encre (et fait encore, la preuve !) dans le monde de l’audio c’est le terme « Hi-Res », contraction de High Resolution… car à l’instar de vos yeux, vos oreilles aussi ont le droit à la haute définition. Nombreux sont les gens à se déchirer sur le bien-fondé et l’intérêt réel de la chose. Le marketing a-t-il encore frappé ? À titre personnel, j’ai choisi mon camp depuis déjà bien longtemps.
Le terme Hi-Res est utilisé pour englober toutes sources audio ayant pour caractéristique commune de faire mieux que le CD sur le plan de l’échantillonnage et de la résolution.
L’échantillonnage consiste à transmettre un signal en capturant des valeurs à intervalles réguliers. Car pour numériser le son, il faut coder (en série de bits donc) des échantillons de la musique qui sont prélevés à intervalles réguliers.
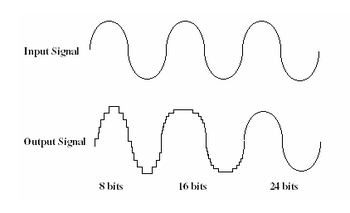
Courbes de signal audio
La résolution (le terme approprié est quantification) est la profondeur de Bits avec laquelle cet échantillonnage a été fait. Plus il y a de Bits, plus il y a de points de mesures, plus le signal est « juste », correctement retranscris.
Un CD est 16 Bits/44.1Khz. Cela veut dire que le signal audio a été échantillonné (comprendre découpé) 44100 fois par seconde avec une profondeur (précision) de 16 Bits.
Pour information, 16 Bits c’est 65536 possibilités de valeurs de niveau sur la courbe du signal audio. « Ce qui est bien mais pas top » !
L’Hi-Res, quant à lui, propose au moins du 24 Bits soit 16.777.216 points de mesure avec un échantillonnage pouvant aller de 44kHz à 192kHz. Et oui, la musique c’est aussi une histoire de mathématiques !
Mais est-ce vraiment meilleur ?
D’un point de vue technique, tous les enregistrements sont réalisés en 24 Bits et reconvertis en 16 pour pouvoir être gravé sur CD. La raison est simple : Le 24 Bits offre beaucoup plus de latitude en termes de mixage pour un ingénieur du son. Plutôt que d’équilibrer les volumes sonores sur 96 dB, il peut le faire sur 144. Les potards peuvent donc être placés de façons plus précise et les effets derrières chaque instrument sont potentiellement bien plus nuancés. Le rapport signal / bruit est alors meilleur, cela permet de générer beaucoup moins de souffle car on évite de s’approcher des 0 dB, et donc d’induire de la distorsion, comme on serait obligé de le faire avec du 16 Bit.
De plus, le fait d’éviter la conversion 24 -> 16 Bits permet de s’affranchir des problèmes de bruit numérique que cela engendre (artefacts audio dépendant des fréquences). Tout passage d’un signal à une résolution inferieure demandera au technicien de rajouter un bruit de fond (si, si) pour rendre ces aberrations non audibles : le tramage (aussi appelé technique du dithering).
Qui de mieux qu’un Nantais dont c’est accessoirement le métier pour illustrer mes propos ? C’est donc Dj Atom* (membre des C2C, de Beat Torrent, quadruple champion du monde de DJ par équipe, producteur et ingénieur du son de formation) que j’ai interrogé sur l’intérêt de l’Hi-Res. Pour lui, cela offre « plus de dynamique et une meilleure restitution des sons à niveau très faible, comme on peut en avoir sur des orchestres classique ou bien dans du mixage pour le cinéma par exemple. Pour la musique actuelle dans laquelle on retrouve finalement assez peu de dynamique, l’intérêt est moindre (en termes de dynamique en tout cas), sauf pour de l’enregistrement (il faut être capable de pouvoir capter les sons très bas ainsi que les sons très haut sans risquer de saturer). Le format de support final étant le 16 bit (ndlr : pour un pressage CD) il est néanmoins important d’ajouter un bruit numérique appelé dither qui, pour faire court, masque le bruit généré par le passage de 24 à 16 bits et détériore de facto la qualité du fichier natif ».
L’échantillonnage a aussi son importance, mais dans une moindre mesure. Le théorème de Nyquist-Shannon démontre le fait que « l’échantillonnage d’un signal exige un nombre d’échantillons par unité de temps supérieur au double de l’écart entre les fréquences minimale et maximale qu’il contient » (source Wikipédia). Pour éviter de perdre la moitié des lecteurs (la moitié qui était au fond de la classe en cours de maths…), je vais vulgariser un peu : partez du principe que si vous découpez la musique 100 fois par seconde ( 100 Hz ), toutes les fréquences au-dessus de 50 Hz passeront à la trappe.
Avec les 44kHz, nous sommes déjà aux limites de l’audible mais les puissances de calculs actuelles nous autorisent à plus échantillonner.
*Retrouvez (une petite partie de) l’univers de DJ Atom :
Clip Down the Road des C2C
2006 DMC World Team Championship Performance
Son SoundCloud
Sa page Facebook
Son compte Twitter
